- Qr Householder Matlab Code
- Householder Qr Factorization
- Qr Householder Factorization
- Householder Reflection Matrix
$initialize$So far, we have only shown existence , but How do we compute QR decompositions?
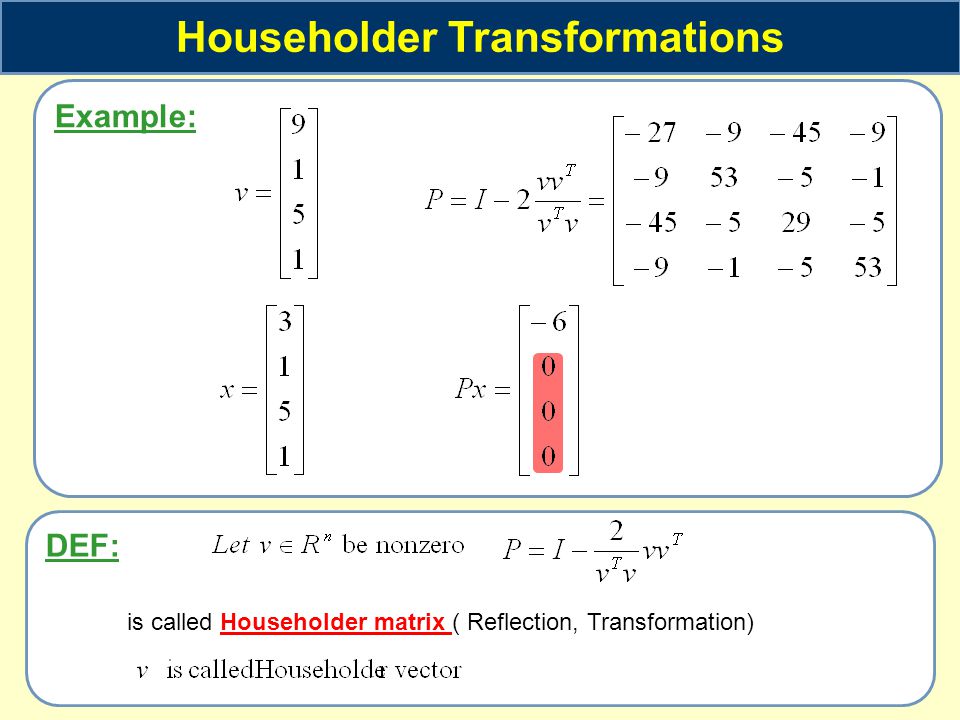
Householder Reflections
Householder reflection is $H=I-2vv'$ where $norm v2=1$ which reflects over hyperplane orthogonal to $v$
A = QR: This factorization can be constructed by three methods: 1. Givens † Property 3.3 (Reduced QR) Suppose the rank of A 2 Rm£n is n for which A = QR is known. Then A = QR where Q and R are submatrices of Q and R given respectively by Q = Q = Q(1: m;1: n); R = R(1: n;1: n): Moreover Q has. The Householder Algorithm. Compute the factor Rof a QRfactorization of m × n matrix A(m ≥ n). Leave result in place of A, store reflection vectors vkfor later use Algorithm: Householder QR Factorization.
Lemma. Householder reflections are orthogonal matrices
Proof. $~$ HOMEWORK
We use a series of Householder reflections to reduce $APi$ to an upper triangular matrix, and the resultant product of Householder matrices gives us $Q,$, i.e. $$underbrace{H_rcdots H_1}_{Q'}APi=R$$
First, find $H_1$ that makes every entry below $R_{11}$ zero,
begin{align*}
H_1a_1&=R_{11}e_1
R_{11}e_1&=a_1-2v_1v_1'a_1
v_1(underbrace{2v_1'a_1}_text{scalar})&=a_1-R_{11}e_1
implies~v_1&=frac{a_1-R_{11}e_1}{norm{a_1-R_{11}e_1}2}
implies~R_{11}e_1&=pmnorm{a_1}2
v_1&=frac{a_1-norm{a_1}{}e_1}{norm{vphantom{big };!a_1-norm{a_1}{}e_1}2}
implies H_1&=I-frac{(a_1-norm{a_1}{}e_1)(a_1-norm{a_1}{}e_1)'}{norm{vphantom{big };!a_1-norm{a_1}{}e_1}{}_2^2}
end{align*}
Then, we have
$$H_aAPi~=~defhmatres{{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!mat{&&&tilde{A}_2&&&}end{matrix}end{matrix}}}left[{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!underbrace{mat{&&&tilde{A}_2&&&}}_text{repeat on these}end{matrix}end{matrix}}^{vphantom{Big }}right]$$
Givens Rotations
Givens rotations $Gij$ where $Gij$ is the identity matrix except
- $Gij_{ii}=Gij_{jj}=lambda$
- $Gij_{ij}=sigma$
- $Gij_{ji}=-sigma$


$$text{for example, },G^{(2,4)}=mat{1&0&0&00&lambda&0&sigma0&0&1&00&-sigma&0&lambda}$$
HOMEWORK $~$ Show that Givens rotation is orthogonal when $sigma^2+lambda^2=1$
We can also use Givens rotations to compute the decomposition, so that $$underbrace{G_Tcdots G_1}_{Q'}APi=R$$
To find $G_1$, we look for a Givens rotation $G^{(1,2)}$ that will make the entry in row 2 column 1 of the product equal to zero. Consider the product with the following matrix $M$ $$mat{lambda&sigma-sigma&lambda},mat{M_{11}&M_{12}&cdots&M_{1m}M_{21}&M_{22}&cdots&M_{2m}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=mat{hphantom{-}lambda M_{11}+sigma M_{21}&hphantom{-1}lambda M_{12}+sigma M_{22}&cdots&hphantom{-1}lambda M_{1m}+sigma M_{2m}-sigma M_{11}+lambda M_{21}&-sigma M_{12}+lambda M_{22}&cdots&-sigma M_{1m}+lambda M_{2m}}$$
To find $G_1$, we solve $$begin{matrix}begin{split}-sigma M_{11}+lambda M_{21}&=0text{s.t. }~~~~~~~~~~~~~sigma^2+lambda^2&=1end{split}end{matrix}~~~~~~~implies~~~~~~~begin{matrix}lambda=frac{M_{11}}{sqrt{M_{11}^2+M_{21}^2}}~~~text{and}~~~sigma=frac{M_{21}}{sqrt{M_{11}^2+M_{21}^2}}end{matrix}$$
Now, we can repeat this process to successively make all entries below the diagonal zero, giving us a QR decomposition.
HOMEWORK
- Determine the computational complexity for QR decomposition using
- Gram-Schmidt
- Modified Gram-Schmidt
- Householder reflections
- Givens rotations
- Compare the complexity of Householder vs Givens for a sparse matrix
- Implement QR decomposition using Householder reflections, (input matrix A of full column rank and output Q,R)
- Repeat 3 using Givens rotations
$$~$$
'Large' data least squares
$AinRnm$, where $ngg m~~$ (which is a different situation than $mgg n$)
Optional reference : 'Incremental QR Decomposition' , by Gentleman.
We can apply QR decomposition to solving the least squares equation $Ax=b$ since
begin{align*}
hat{x}&=(A'A)inv A'b
&=((QR)'(QR))inv(QR)'b
&=(R'cancel{Q'Q}R)inv R'Q'b
&=(R'R)inv R'Q'b
&=Rinvcancel{(R')inv R'}Q'b
&=Rinv Q'b
end{align*}
We need to find $Rinv$ and $Q'b$. To do so, consider just the first $m!+!1$ rows of the matrix $mat{A&b},$ and perform QR decomposition to get $$mat{tilde{R}&tilde{Q}'tilde{b}0&tilde{s}}$$ Then, we add one row at a time to the bottom and perform Givens rotations so that $$mat{tilde{R}&tilde{Q}'tilde{b}0&tilde{s}a_{m+2}&b_{m+2}}~~~implies~~~mat{tilde{R}_{m+2}&tilde{Q}_{m+2}'tilde{b}_{m+2}0&tilde{s}_{m+2}0&0}$$
$$~$$
Section7.5QR decomposition by Householder reflectors
¶Another algorithm for determining the (QR) decomposition of a matrix which requires fewer operations and is less susceptible to rounding error is the method of Householder reflectors. The method depends upon the following theorem.
Given two such vectors (vec{x},vec{w}inR^ntext{,}) define (vec{v}=vec{w}-vec{x}text{,}) and consider the matrix
While it may be confusing to think that this is a matrix, recall: since (vec{v}) is an (ntimes 1) column matrix, (vec{v}vec{v}^T) is an (ntimes n) symmetric matrix. In fact,
Qr Householder Matlab Code
and

A matrix satisfying (P^2=P) is called a projection matrix. The purpose of using (P) is that (vec{x}-Pvec{x}) is the projection of (vec{x}) onto (vec{w+x}text{,}) and therefore (vec{x}-2Pvec{x} = vec{w}text{!})
Householder Qr Factorization
For brevity, I'll refer to the (QR) decomposition by Householder reflectors as HHQR. The process of HHQR for a matrix (A) iterates through the columns of (A) just like Gram-Schmidt, but with far less numerical instability. We'll explain the process without use of an example, as the process becomes extremely unwieldy in exact arithmetic.
Suppose we begin with a (mtimes n) matrix 1 The discussion of the method contained here originally appears in Timothy Sauer's excellent Numerical Analysis, 2nd edition. (A = [a_{i,j}]text{,}) where (m>ntext{.}) We will choose as our first vector (vec{x}_1 = vc{a_{1,1},a_{2,1},ldots, a_{m,1}}text{,}) the first column of (Atext{.}) Since we desire to reflect it onto a coordinate axis vector of the same magnitude, we can choose (vec{w_1}=vc{pmabs{vec{x}_1},0,0,ldots,0}text{.}) Since subtracting nearly identical floating point numbers is problematic and leads to rounding error, we will choose the sign of the first coordinate of (vec{w}_1) to be the opposite of the sign of the first coordinate of (vec{x}_1text{.}) This allows us to determine the first Householder reflector (H_1) such that (H_1vec{x}_1 = vec{w}_1text{.}) Now, putting (R_1 = H_1A) gives us a matrix whose first column is (vec{w}_1text{,}) by construction; notably, this is the first iteration and in the first column (R_1) is the start of an upper triangular matrix. Specifically, if we write (R_1=[r_{i,j}]text{,}) we have (r_{i,1} = 0) whenever (i>1text{.})
Qr Householder Factorization
In order to continue this process, we will produce from (R_1) a new matrix (R_2=[r_{i,j}]) which has (r_{i,j}=0) whenever (i>j) and (jleq 2text{.}) We do so by ignoring the first row and column of (R_1text{;}) doing so gives us (R'_1text{,}) an ((m-1)times(n-1)) matrix. If we let (vec{x}_2) be the first column of (R'_1) and (vec{w}_2=vc{pmabs{vec{x}_2},0,0,ldots,0}text{,}) we can find the Householder reflector (hat{H}_2) such that (hat{H}_2vec{x}_2=vec{w}_2text{.}) Say then that (hat{H}_2 = [hat{h}_{i,j}]text{.}) We will create our full reflection matrix by inserting (hat{H}_2) into the bottom right corner of an identity matrix. Here is the formula for (h_{i,j}) along with the more intuitive picture diagram:
Householder Reflection Matrix
Then (R_2=H_2R_1=H_2H_1Atext{.})
We continue this process in the way established: at each step, we reflect the first column of a submatrix onto a coordinate-axis vector of the same length, flipping signs of the first coordinate, and after processing (n) columns in this way we have (R=H_nH_{n-1}cdots H_2H_1Atext{,}) which is an upper triangular matrix. Moreover, the matrices (H_j) are all orthogonal matrices, so (H_j^{-1}=H_jtext{.}) Hence we obtain